Publication: 2024-08-03

How to implement a Buddy allocator

Memory allocation strategies are interesting because they often make compromises between performance and memory overheads, depending on whether allocations and deallocations are made predictably. For instance, an Arena allocator is great if all allocations are kept alive until the very end when they are all deallocated, and a Pool allocator is great if all allocations have the same size.

Somewhat in the middle, the Buddy allocator tries to be generic regarding allocation patterns, without expecting a specific timing for allocations and deallocations, nor using a fixed size. There are quite a bit of resources on the principles of the Buddy allocator, but I did not find a discussion about a specific implementation. So, given that I needed one for work, I rolled my own, and this article describes the process, and the data structures and algorithms used. This results in a pretty long article! 😅

The implementation is available online, in the public domain (UNLICENSE).

How a Pool allocator works

To discuss the inner workings of the buddy allocator, let's first examine the simpler Pool allocator, which inspires the Buddy allocator.

Divide a big chunk of memory (eg. 8 MiB) into slots of equal sizes (eg. 512 slots of 16 kiB each).
Attribute an integral ID to each slot (eg. between 0 and 511 inclusive).
On initialization, put the IDs of all slots into a list named the "freelist".
On allocation, extract the front ID of the freelist, and return the corresponding slot address to caller.
On deallocation, put the ID of the released slot into the freelist.

The obvious limitation of the Pool allocator is that it can only return fixed-size slots: ask for bigger size and the allocation fails, ask for smaller size and you waste memory. Thus, it is to be used in particular scenarios where the allocations are known to be of the same size, eg. as the backing allocator for the nodes of a tree or for an unordered set/map.

A few implementation notes on the Pool allocator:

The deallocation should put released slots to the front of the freelist, such that the next allocation reuses memory which was recently accessed, to benefit from the hardware memory caches.
The freelist can be implemented as a separate stack-like array, in which case using slot IDs (eg. up to 1023) reduces the memory consumed by metadata (eg. 16-bit integers instead of 64-bit pointers).
Alternatively, the freelist can be implemented as a singly-linked list, whose nodes are stored directly in their corresponding slot, because a slot referred by the freelist is, in theory, not to be used. In which case, the Pool allocator has 0% memory overhead! However, in practice, use-after-free bugs (when some code writes into a deallocated slot) occur, in which case the freelist becomes garbage and the next allocation will make the program crash mysteriously (high risk, high reward I suppose 😄).
The slots are actually not required to be part of a single big chunk of memory, but this allows better memory locality, thus better performance.

How a Buddy allocator works

The Buddy allocator mitigates the downsides of the Pool allocator by allowing multiple sizes of allocations. The basic idea can be resumed as intertwining pools of different sizes and move slots between them:

Choose a minimal allocation size (eg. \(\text{minAllocSize} = 16 \text{ KiB}\)) and a maximal allocation size (eg. \(\text{maxAllocSize} = 8 \text{ MiB}\)), both must be powers of two.
Subdivide a big buffer (eg. \(\text{totalRangeSize} = 128 \text{ MiB}\)) into slots of maximal allocation size (eg. 16 slots of 8 MiB).
On initialization, create a freelist per powers of two between minimal and maximal allocation size, inclusive (eg. 10 freelists). All freelists are empty, except for the one corresponding to maximal allocation size, which contains all slots from step 2.
On allocation, round the requested size to the next power of two, and extract a slot ID from the corresponding freelist. If the freelist was empty, search a slot from another freelist, and split it into smaller slots, one of them is returned to the caller.
On deallocation, if the released range is next to another free slot of same size, coalesce the two ones in a bigger slot, to be added to the freelist.

Compared to the Pool allocator, the main difficulty added is the logic to split and coalesce adjacent slots between different freelists. The Buddy allocator pairs the slots of one pool two-by-two, to form a single slot in the next pool: thus, each slot can only be coalesced with a single other slot, its "buddy" slot. See the illustration below:

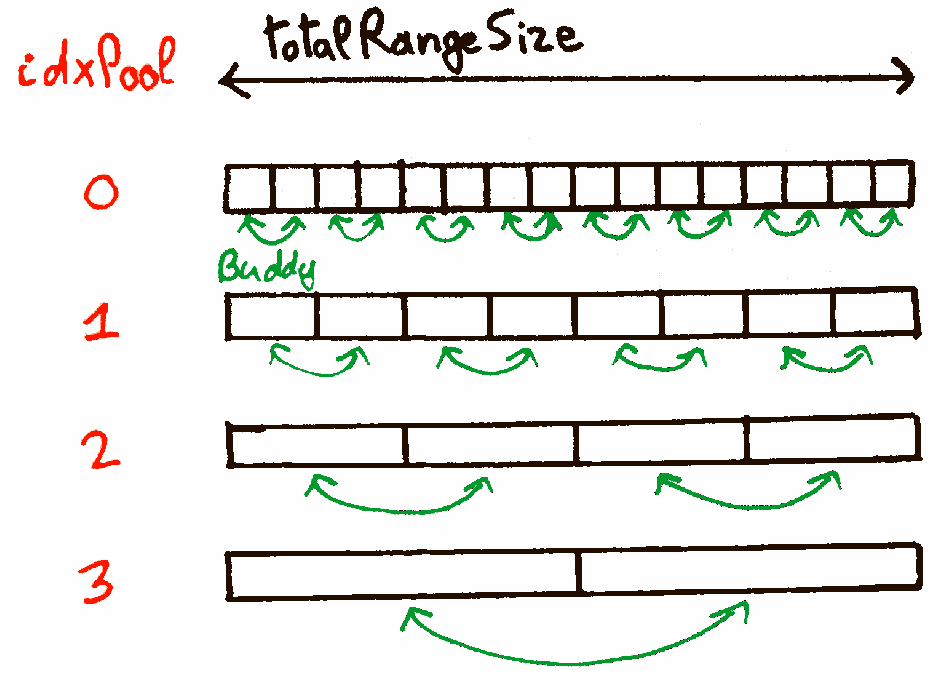
The rest of the blog post discusses how to implement this logic, and the data structures needed.

The API to be implemented

The API I propose is freestanding, pointer-unaware and minimalist. The caller is responsible for converting between offsets and pointers (eg. by adding or substracting a base pointer pStart), and to allocate memory for metadata. Thus, a wrapper can implement whatever memory backing it wants: in-memory buffer, virtual allocations, GPU allocations... At my workplace, I used it for determining file offsets to implement a system akin to memory swapping.

struct JvBuddyParams
{
    int64_t minAllocSize;
    int64_t maxAllocSize;
    int64_t totalRangeSize;
};

struct JvBuddySlot
{
    int64_t offset;
    int64_t size;
};

/// Returns the number of bytes needed for `pMetadataStorage` in `jvBuddyInit()`, or `-1` on error.
int64_t jvBuddyGetMetadataSize(JvBuddyParams params);

/// Initializes the buddy allocator, returns `NULL` on error.
JvBuddy* jvBuddyInit(JvBuddyParams params, void* pMetadataStorage);

/// Returns a new slot of at least given size, or `{0,0}` on failure.
JvBuddySlot jvBuddyAlloc(JvBuddy* pBuddy, int64_t size);

/// Deallocates a slot obtained previously by `jvBuddyAlloc()` and starting at `offset`.
/// Returns the size of the slot freed, or `0` if `offset` was invalid.
int64_t jvBuddyFree(JvBuddy* pBuddy, int64_t offset);

/// Finds the slot which contains given `offset`, and fills `pSlot` and `pbAllocated`.
/// Returns `true` on success, `false` if `offset` was invalid.
bool jvBuddyQuery(JvBuddy* pBuddy, int64_t offset, JvBuddySlot* pSlot, bool* pbAllocated);

The data structures

The buddy allocator can allocate slots of sizes which are powers-of-two between minAllocSize and maxAllocSize. Each possible size is served by a different pool, with its own freelist: we have poolCount \(= 1 + \log_2\frac{\texttt{maxAllocSize}}{\texttt{minAllocSize}}\). Due to the coalescing of slots, slots can be removed from their freelist arbitrarily (not necessarily at the front). This prevents stack-like arrays and singly-linked lists: the freelists must be implemented as double-linked lists.

Conceptually, the totalRangeSize is divided into subranges of minAllocSize bytes each. A slot may be comprised of multiple such subranges. Each slot is identified by the index of the first subrange they contain, as a 16-bit integer, where UINT16_MAX = 65535 is a special value for "invalid slot". This limits the capacity of the Buddy allocator: it can manage at most totalRangeSize ≤ 65535 * minAllocSize. If more is needed, a 32-bit integer can be used, but it almost doubles the metadata storage needed.

We first store the state of each slot, which contains which pool it belongs to, and whether it is currently allocated. The access must be fast, and I want the metadata to have fixed storage, which directed me to the choice of an array, indexed as discussed before.

struct _JvInfo
{
    uint8_t bAllocated : 1;
    uint8_t bFreelist : 1;
    uint8_t idxPool : 6;
};

uint16_t subrangeCount;
_JvSlotInfo* pSlotInfos; // [idxSlot] in 0..subrangeCount-1

A slot whose first subrange's index is idx will store its metadata in pSlotInfos[idx]. The other subranges for this slot are recognizable because both bAllocated and bFreelist will be false.

Τhen, we need to store the freelists, implemented as double-linked lists. I also use an array accessed by the same conventions as pSlotInfos. If for a given index, pSlotInfos[idx].bFreelist is false, then pSlotLinks[idx] stores meaningless info, and should not be accessed. Finally, we need to store the front of the freelists, such that we can insert to and remove from the front of the list.

struct _JvDlist
{
    uint16_t idxHead;
    uint16_t idxTail;
};

struct _JvLink
{
    uint16_t idxPrev;
    uint16_t idxNext;
};

uint8_t poolCount;
_JvDlist* pPoolFreelists; // [idxPool] in 0..poolCount-1
_JvLink* pSlotLinks; // [idxSlot] in 0..subrangeCount-1

We could put idxSlotPrev and idxSlotNext into the same _JvInfo structure as before, but alignment would waste memory, and this permits more cache friendly access to the pSlotInfos array, which is accessed multiple times per API call.

To sum it up, we have:

uint16_t pPoolFreelists[poolCount] (\(2 \times (1 + \log_2\frac{\texttt{maxAllocSize}}{\texttt{minAllocSize}})\) bytes)
_JvInfo pSlotInfos[subrangeCount] (\(\frac{\texttt{totalRangeSize}}{\texttt{minAllocSize}}\) bytes)
_JvLink pSlotLinks[subrangeCount] (\(4 \times \frac{\texttt{totalRangeSize}}{\texttt{minAllocSize}}\) bytes)

Given that the pPoolFreelists storage is negligeable, the memory overhead (relative to totalRangeSize) is \(\frac{500}{\texttt{minAllocSize}} \%\); for instance, if you allocate slots of at least 512 bytes, you have an overhead less than 1% the total memory managed.

Allocation and splitting logic

Given a requested size, in bytes, we must first decide which pool is going to be preferred. _jvLog2 returns the logarithm base-2 of size, rounded up. minAllocLog2 and maxAllocLog2 are respectively the logarithms base 2 of minAllocSize and maxAllocSize ; they are used to transform multiplications and costly divisions into cheap additions, substractions and shifts.

uint8_t sizeLog2 = _jvLog2(size);
if (sizeLog2 > pBuddy->maxAllocLog2) {
    return (JvBuddySlot) { 0, 0 };
}
if (sizeLog2 < pBuddy->minAllocLog2) {
    sizeLog2 = pBuddy->minAllocLog2;
}
uint8_t idxPoolDesired = sizeLog2 - pBuddy->minAllocLog2;

Then, we must extract a free slot from the desired pool, or from a pool with bigger slots. Pools are numbered from 0 (smallest slots) to poolCount - 1 (biggest slots). _jvBuddyRemoveFromFreelist simply removes the slot from the freelist pPoolFreelists[pInfo->idxPool], handling the relink of previous and next slots.

uint8_t idxPool = idxPoolDesired;
uint16_t idxSlot = UINT16_MAX;
for (; idxPool < pBuddy->poolCount; idxPool += 1) {
    idxSlot = pBuddy->pPoolFreelists[idxPool].idxHead;
    if (idxSlot != UINT16_MAX) {
        break;
    }
}
if (idxSlot == UINT16_MAX) {
    // No slot found: out-of-mem.
    return (JvBuddySlot) { 0, 0 };
}
_JvInfo* pInfo = &pBuddy->pSlotInfos[idxSlot];
_jvASSERT(pInfo->bAllocated, ==, false);
_jvASSERT(pInfo->bFreelist, ==, true);
pInfo->bFreelist = false;
_jvBuddyRemoveFromFreelist(pBuddy, idxSlot, pInfo);

If the gotten slot is too big, we split it until having the desired size: every other slot created by these splits are added to their respective freelists. Note the logic to get the index of the buddy slot, based on a XOR, as illustrated in the following image.

while (idxPool > idxPoolDesired) {
    idxPool -= 1;
    uint16_t idxBuddy = idxSlot ^ (1u << idxPool);
    _JvInfo* pInfoBuddy = &pBuddy->pSlotInfos[idxBuddy];
    _jvASSERT(pInfoBuddy->bAllocated, ==, false);
    _jvASSERT(pInfoBuddy->bFreelist, ==, false);
    pInfoBuddy->bFreelist = true;
    pInfoBuddy->idxPool = idxPool;
    _jvBuddyAddHeadToFreelist(pBuddy, idxBuddy, pInfoBuddy);
}

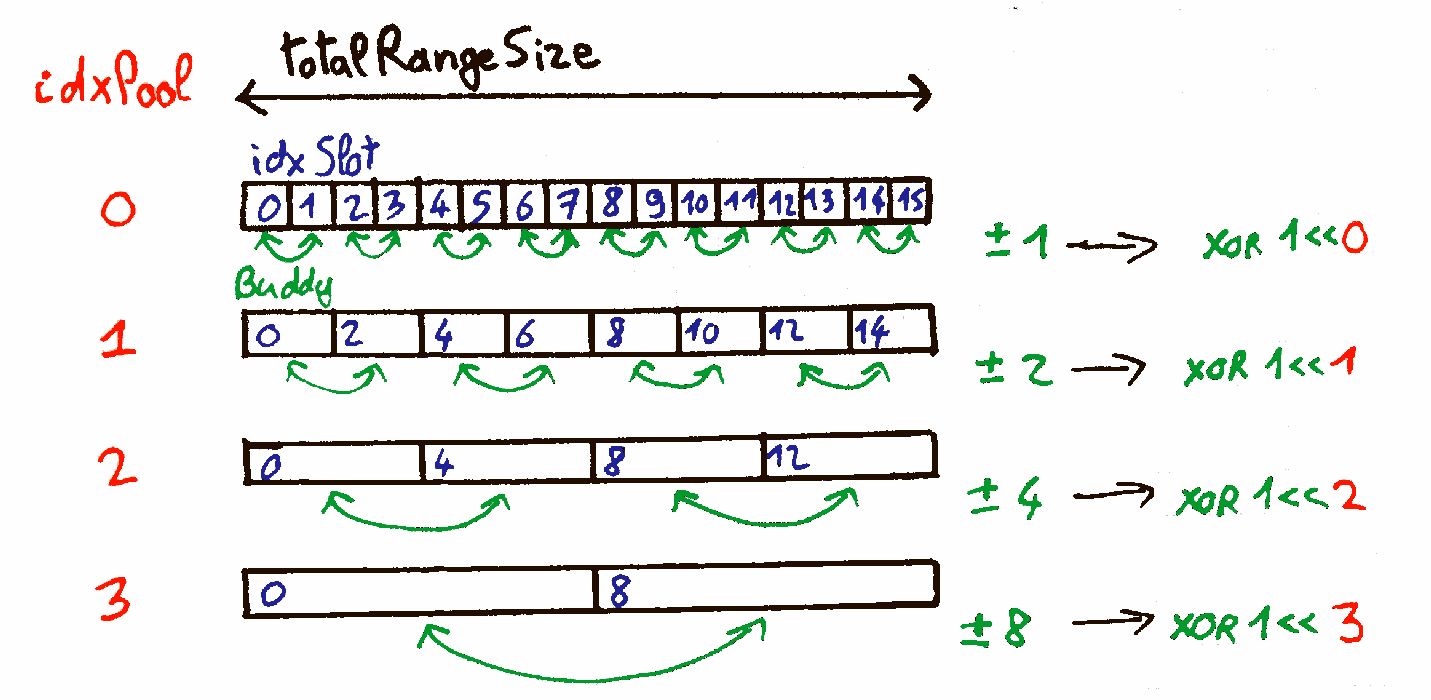
Finally, we simply update the chosen slot's state, and derives the offset and size of the allocation.

pInfo->bAllocated = true;
pInfo->idxPool = idxPool;

JvBuddySlot slot;
slot.offset = (int64_t)idxSlot << pBuddy->minAllocLog2;
slot.size = (int64_t)1 << (pBuddy->minAllocLog2 + idxPool);
return slot;

Deallocation and coalescing logic

The first step is simply to retrieve the size of the allocated slot:

uint16_t idxSlot = (uint16_t)(offset >> pBuddy->minAllocLog2);
_JvInfo* pInfo = &pBuddy->pSlotInfos[idxSlot];
uint8_t idxPool = pInfo->idxPool;
_jvASSERT(pInfo->bAllocated, ==, true);
_jvASSERT(pInfo->bFreelist, ==, false);
pInfo->bAllocated = false;

Then, the coalescing logic takes place. We check whether the buddy of the freed slot is free too (it must be in a freelist, and it must have the same size). In which case, we remove the buddy from its freelist, and we consider now the fusionned slot. We repeat the process while we can, until reaching the maximal slot size.

for (; idxPool < pBuddy->poolCount - 1; idxPool += 1) {
    // See whether the buddy is free, in which case remove it from freelist.
    uint16_t idxBuddy = idxSlot ^ (1u << idxPool);
    _JvInfo* pInfoBuddy = &pBuddy->pSlotInfos[idxBuddy];
    if (!pInfoBuddy->bFreelist || pInfoBuddy->idxPool < idxPool) {
        break; // Buddy not allocated (either not in freelist, or smaller slot)
    }
    _jvASSERT(pInfoBuddy->bAllocated, ==, false);
    _jvASSERT(pInfoBuddy->idxPool, ==, idxPool); // Should not have >
    pInfoBuddy->bFreelist = false;
    _jvBuddyRemoveFromFreelist(pBuddy, idxBuddy, pInfoBuddy);
    // Update idxSlot to the fusion of the two slots.
    idxSlot &= UINT16_MAX << (idxPool + 1);
}

Finally, we add the slot we have (possibly resulting of the coalescing of multiple smaller slots), and we add it to the appropriate freelist:

// Add the new block to corresponding freelist.
pInfo = &pBuddy->pSlotInfos[idxSlot];
_jvASSERT(pInfo->bAllocated, ==, false);
pInfo->bFreelist = true;
pInfo->idxPool = idxPool;
_jvBuddyAddHeadToFreelist(pBuddy, idxSlot, pInfo);
return (int64_t)1 << (pBuddy->minAllocLog2 + idxPoolOld);

Conclusion

While the Buddy allocator is conceptually a simple extension of Pool allocators, splitting and coalescing slots requires specific data structures to be efficient. Moreover, in both times I implemented it (one at work, and one here), there were a few bugs hidden in these 300 lines of code. Fixing them strongly highlights the usefulness of a step-by-step debugger, coupled with unit tests and heavy use of assertions in the implementation.

I have not discussed the implementation of jvBuddyQuery(), which uses a similar loop than for coalescing. Akin to Win32 VirtualQuery, the API allows to iterate over all slots of the Buddy allocator, eg. to measure the total amount allocated currently:

int64_t measureBuddy(JvBuddy* pBuddy)
{
    int64_t count = 0;

    bool bAllocated;
    JvBuddySlot slot;
    int64_t offset = 0;
    while (jvBuddyQuery(pBuddy, offset, &slot, &bAllocated)) {
        if (bAllocated) {
            count += slot.size;
        }
        offset = slot.offset + slot.size;
    }
    return count;
}

My implementation is available in the public domain. If you find it useful, feel free to send me an email or share this article. 😊

Thanks for reading, have a nice day!

Keys	Action
`?`	Open this help
`n`	Next page
`p`	Previous page
`s`	Search