Publication: 2024-06-17
Interpreting decimal strings into floats (Part 1)
Interpreting decimal strings is a common task in programming, wherever a text-based format is used for data : source code, data exchange with JSON, configuration with TOML...
Most implementations I have found are complex (multiple source files, implementing custom types, big lookup tables, thousand line of codes...). There may be the need for a smaller implementation, in the same spirit as the STB libraries. I also wanted to give a go to a low-level problem. Given that this journey was longer than what I expected, I wanted to write about how I tackled the problem, how I reached this implementation, such that to keep and share familiarity with the implementation.
For legibility, I have split the writing into three articles. The third article contains discussion about correctness and performances. I have not copied the entire implementation verbatim in these articles: I recommend to read the C code along the explanations given in these articles, my implementation is available online, in the public domain. Finally, a couple math proofs were put off to the end of the article.
The problem
The problem of interpreting a decimal string as a float can be divided in three parts:
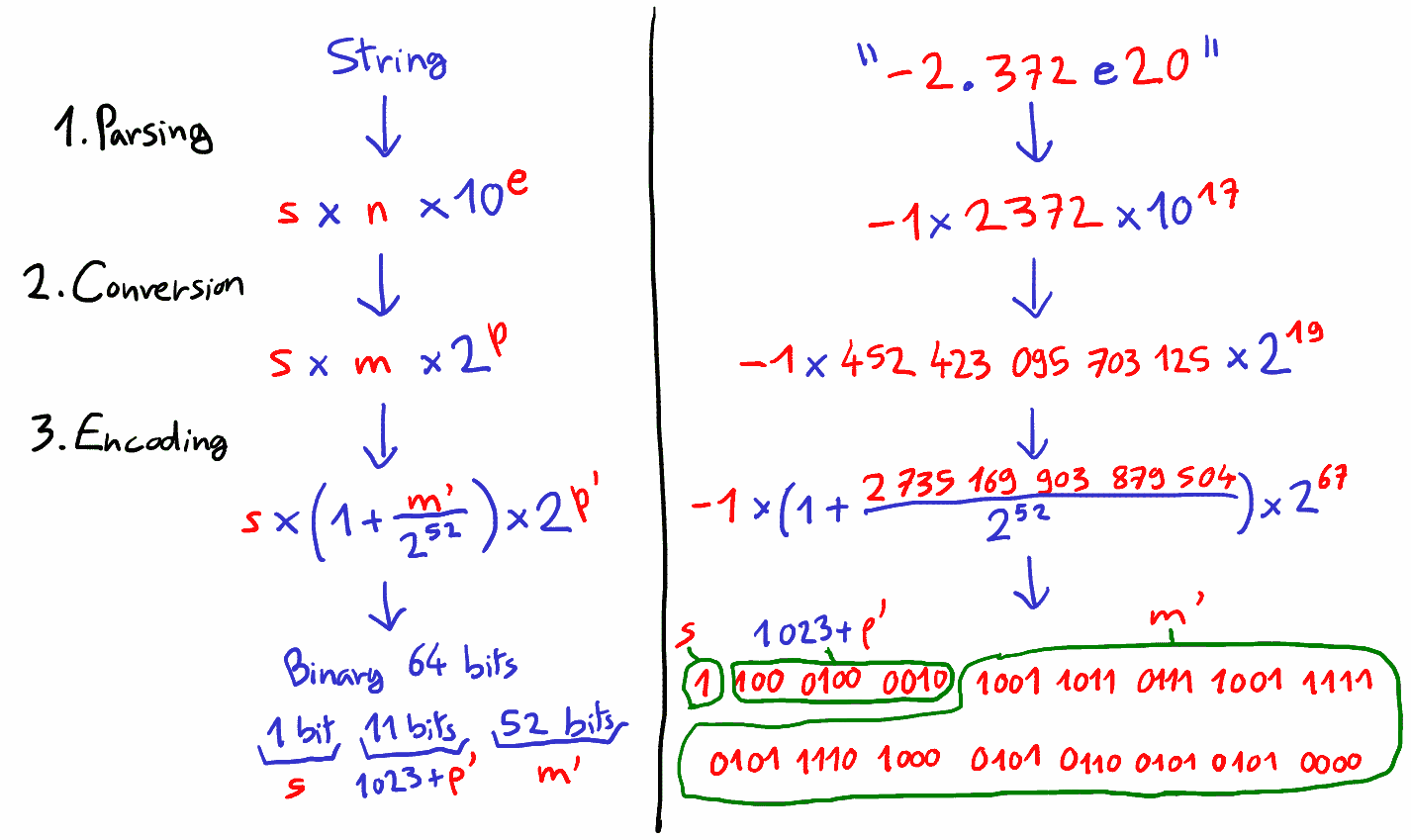
A decimal string contains three parts: a sign \(s = \pm 1\) , an integral part \(n\) and an integer exponent part \(e\) :
Float encodes numbers also as three parts: a sign \(s \pm 1\), an integer part \(m\) and an integer exponent part \(p\), except that a power of two is used:
The main problem is to find \((m,p)\) such that \(m \times 2^p \approx n \times 10^e\). Note that we may only approximate some values for two reasons. First, there are numbers such that \(0.1\) which cannot be represented as \(m \times 2^p\) (Proof 1). Second, the encoding of \(m\) and \(p\) uses a fixed number of bits, limiting the available precision. For instance, to represent the number \(1 + 2^i\) exactly, \(m\) must be represented with at least \(i+1\) bits (Proof 2).
My goal is to solve this problem with a reasonably portable and readable C implementation, without doing memory allocations (thus, we cannot have arbitrary precision), and using only integer arithmetics in order to prove more easily the margin of errors. Given that arbitrary precision is not considered, I expect the parser to not be exact in cases where the input string is particularly precise, or when breaking out ties.
This first blog entry is dedicated to the first step: parsing the string and extracting \((s,n,e)\).
Parsing the string
The strings we want to parse optionally start with a sign, followed by an integer and fractional part, followed optionally by an exponent part:
The syntax does not limit the number of digits in the fractional and exponent parts: but because the implementation has limited precision, we cannot treat arbitrary many digits: the parser must handle properly when too many digits are provided for what is representable internally (overflows).
From this syntax and the concerns about overflows, I use the following architecture, presented as a railroad diagram, with the different parts indicated with green text:
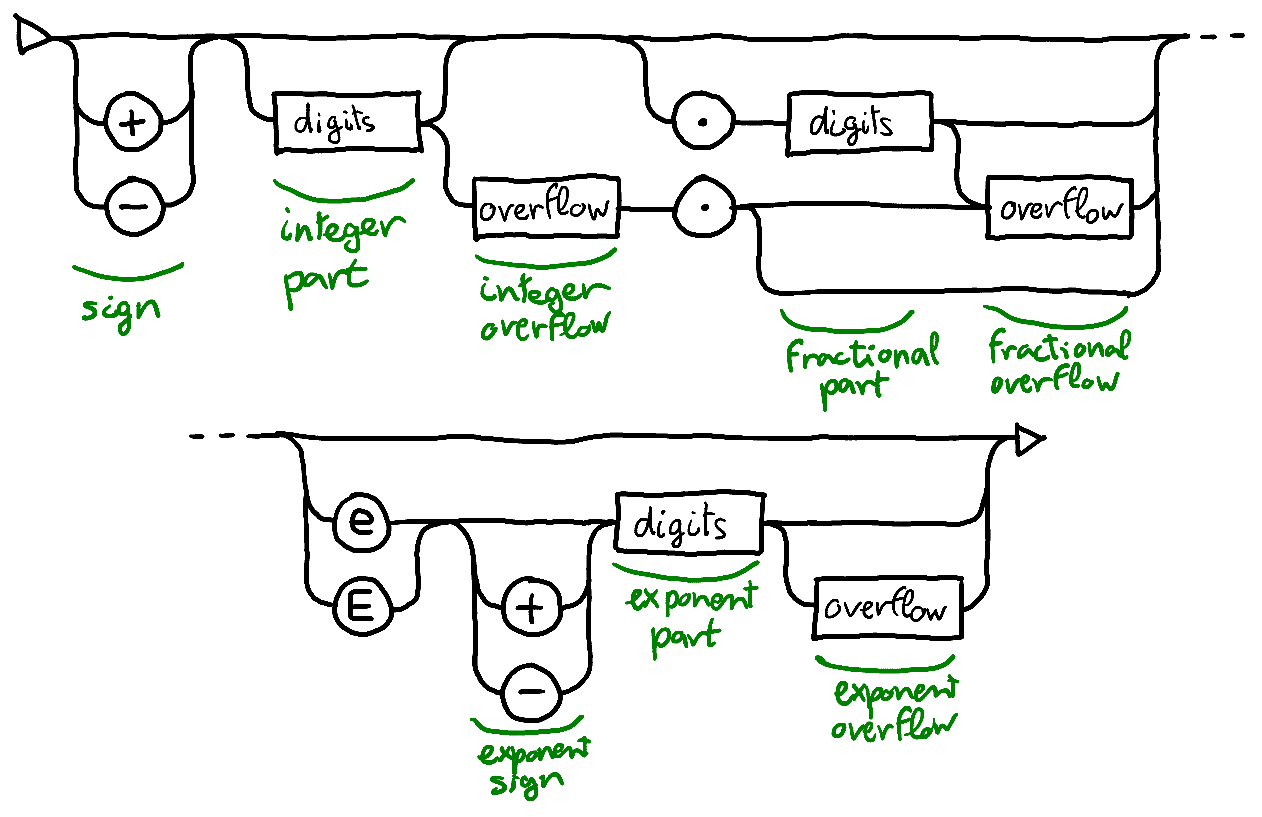
The 8 parts of the parser extracts information from the string:
| Part | Info |
|---|---|
| sign | Sign of value \(s\). |
| integer part | Digits accumulate into \(n\). |
| integer overflow | Each digit will make \(e\) increment. |
| fractional part | Digits accumulate into \(n\), each digit will make \(e\) decrement. |
| fractional overflow | Digits are ignored. |
| exponent sign | Sign of exponent \(e\) . |
| exponent part | Digits accumulate into \(e\). |
| exponent overflow | Value is considered zero or infinity. |
The C implementation follows closely this architecture, as a state machine. I have chosen to delimit each part with goto, which I find legible enough in this context, given that the flow only goes forward. You may prefer more high-level primitives, such as functions or methods, but when expressed in C, they implied more complex function calls which I considered to degrade the readability.
The algorithm keeps the following state:
| Name | C Type | Comment |
|---|---|---|
pStr |
char const* |
The string to parse. |
strSize |
ptrdiff_t |
Number of characters in the string. |
i |
ptrdiff_t |
Position of current character in the string. |
c |
char |
Synonym for pStr[i], for readability. |
bNegative |
bool |
Whether the string starts with minus -. |
bExpNegative |
bool |
Whether the exponent starts with minus -. |
n |
uint64_t |
Accumulator for integer and fractional parts. |
exp |
int64_t |
Accumulator for exponent part. |
expBias |
int64_t |
The bias introduced by integral overflow and fractional part, to be added to exp. |
pStr and strSize are the arguments of the parsing, the other variables are initialized to zero/false.
bNegative, bExpNegative, n, exp and expBias are the outputs of parsing.
Nothing special to be said about the parsing: a bunch of if , one character at a time. Two particularities occur regarding overflow handling for \(n\).
Overflow logic
First, to detect overflow, I use add-with-carry and multiply-extended. Both take two 64-bit inputs and produce a 128-bit output. They correspond to a single cycle instruction on 64-bit machine, but in C they are only exposed with compiler intrinsics, different per compilers, for instance with MSVC:
#include <intrin.h>
static inline uint64_t _jvAdd64(uint64_t a, uint64_t b, uint64_t* low)
{
return _addcarry_u64(0, a, b, low);
}
static inline uint64_t _jvMul64(uint64_t a, uint64_t b, uint64_t* low)
{
uint64_t high;
*low = _umul128(a, b, &high);
return high;
}
Second, among the digits skipped due to overflow, we can use the first one to round our result: if the first skipped digit is higher than \(5\), we increment \(n\). This easy trick halves the margin of error for this step. But this increment may also overflows, so it must be handled gracefully too.
The resulting code to accumulate a character digit c in accumulator n is:
// Make a copy, in case computations overflow.
uint64_t n2 = n;
// n2 = (10 * n2) + (c - '0')
uint64_t overflow = _jvMul64(n2, 10, &n2);
overflow += _jvAdd64(n2, c - '0', &n2);
if (overflow > 0) {
// Add bias towards the correct value
overflow = _jvAdd64(n, c >= '5', &n);
if (overflow) {
// If overflow, 'n' was 2^64-1: approximated value is 2^64.
n = 1844674407370955162; // round(2^64/10)
expBias += 1;
}
goto integer_overflow;
}
// Apply result, if there was no overflow.
n = n2;
The exponent overflow is easier to handle. If the accumulated exp is higher than a upper bound, for instance \(1\ 000\ 000\ 000\), I approximate the float to represent infinity, which is true except if the string has one billion leading zeroes past the point.
Margin of error

Let's compute the margin of error \(\varepsilon = |\frac{N-N'}{N}|\), with :
- \(N\): the exact integer represented by the string (without considering the point, which is only relevant for determining the exponent).
- \(i\): the number of skipped digits.
-
\(n\): the actual integer stored in the accumulator, less than \(2^{64}\).
-
\(N' = 10^i \times n\) : the represented number, to be compared with \(N\).
First, if we have \(N < 2^{64}\), no overflow occurs, no digits are skipped (\(i = 0\)), thus \(N = n = N'\), the error is \(\varepsilon = 0\).
Else, the number of digits to be skipped is the smallest integer \(i\) such that \(N\) divided by the power of two will not overflow a 64-bit integer:
Because \(i\) must be the smallest integer possible, we get:
We can choose \(n\) as either \(\lfloor \frac{N}{10^i}\rfloor\) or \(\lfloor \frac{N}{10^i}\rfloor + 1\), depending on whether the remainder \(r = N \text{ mod } 10^i\) is greater than \(0.5 \times 10^i\) (i.e. is the first skipped digit bigger than 5).
If \(r < 0.5 \times 10^i\), we choose \(n= \lfloor \frac{N}{10^i}\rfloor\) , the difference \(N - N'\) is:
Else \(r \ge 0.5 \times 10^i\), we choose \(n= \lfloor \frac{N}{10^i}\rfloor + 1\) :
So in both cases, the absolute difference is less than \(0.5 \times 10^i\). Thus we can compute the error:
The relative error is \(\varepsilon \approx 2.71 \times 10^{-19}\) , which means a precision of 18 decimal digits. Alternatively, \(\varepsilon = 1.25 \times 2^{-62}\), which means a precision of 61 bits.
Summary
With this blog post, we have done one third of the road to interpret decimal strings into floats. We know have expressed the string as a tuple \((s, n, e)\), such that the encoded number has a relative error \(\varepsilon \le \frac{5}{2^{64}}\).
In the next blog post, we will tackle the internal computations to convert our base-10 tuple into a base-2 tuple.
Thanks for reading, have a nice day!
Proofs
Proof 1: Why \(0.1\) cannot be represented as \(n \times 2^p\)
We search \((n,p)\) two integers such that \(0.1 = n \times 2^p\).
This equation is equivalent to \(2^{-p} = 10 \times n = 5 \times 2 \times n\).
That is, we must find an integral power of two which has the prime factor \(5\).
But an integral power of two has only a single prime factor: \(2\).
Thus, the equation cannot be solved.
Proof 2: Why \(1+2^i\) needs \(m\) to be \(i+1\) bit long
We search the smallest integer \(m\) such that \(1 + 2^i = m \times 2^p\).
Because \(1+2^i\) is odd, we cannot have \(p > 0\).
If \(p < 0\), we can get a smaller \(m\) by dividing it by two, and incrementing \(p\).
Thus, \(p\) must be equal to zero to get the smallest integer \(m\).
This means that \(m = 1 + 2^i\).
The numbers representable on \(k\) bits are \(m < 2^k\).
We have \(2^i < m < 2^{i+1}\).
Thus, \(m\) must be represented with at least \(i+1\) bits.
Attributions
"Math time" image : Math Vectors by Vecteezy